What is a Q-Field?

I have frequently talked about the interpretation of quantum physics implying that “everything is a quantum wave”. Here I’d like to explain this a bit better and, more importantly, tell you about some problems with this picture of the universe. Yes, the fact that I claim it to be the best representation of natural phenomena we’ve got doesn’t mean that it’s not problematic. And one of these problems may well lead to the downfall of quantum physics and the emergence of our next theory. So, a subject definitely well worth thinking about…

Photo by Zoltan Tasi on Unsplash

First, what is a classical field? In the simplest case it is a single number assigned to each point in space and changing in time. That’s sounds simple. Think of the field of water waves in the ocean. At each point we can specify the height of the water – say with respect to some fixed reference like the seabed – and then we specify further how this height changes in time.

However, there is an extra constraint that makes our life easier. Not any assignment of numbers will do. Waves in physics satisfy a very specific constraint. This constraint is called a wave equation. To give you an easy way to visualise this, think about one dimension of space changing in time (so one dimension of time). The wave equation now stipulates that if you look at one point x at time t, the average of the field at neighbouring points (x +dx and x-dx and at time t) is the same (in suitable units) as the average of the field of neighbouring times (t+dt and t-dt both at the location x). Here dx is a small (mathematicians call this “infinitesimal”) distance and dt is a small (infinitesimal) time interval.

Now, in quantum physics, there is an extra simplification, but – then, sadly – accompanied by a complication too, with respect to classical fields. As far as the simplification is concerned, everything in quantum physics behaves like a wave; everything obeys a wave equation. This is simply mind-blowing since both particles and waves are now just waves (this is why I called this interpretation the “everything is a quantum wave” interpretation). I’ve written about this when I waved “Goodbye to the Wave-Particle Duality”.

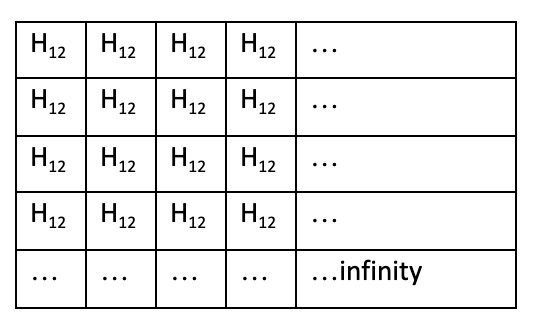
But, and this is the complication bit, these quantum waves cannot be specified by just giving one number at every place. We need to specify what Dirac called a q-number. And this is actually a two-dimensional table of numbers, infinite in each of the two directions. So, rather than saying the height of water is 5 meters, we now have to say

And this has an “infinity squared” of numbers in it (entities of this kind are called matrices). The reason for this escalation of numbers is that – in quantum physics – things like the height of the wave and the speed at which the wave changes cannot be specified at the same time. This is Heisenberg’s uncertainty principle. So, one infinity squared is required to specify the height of the wave and another infinity square to specify its speed (or “phase” to be more precise).

When I give talks on this topic – and I did one recently at the Royal Institution in London – many audience members are surprized that these infinite matrices appear in quantum physics. The reason why everyone is surprized is that this is not how quantum mechanics is usually popularized.

Take for instance Richard Feynman, a phenomenal lecturer, one of the most talented post-war physicists, and a person who brought physics to the masses more than anyone else since Michael Faraday. He said that the double slit experiment contained all quantum mysteries. When what we think of as a particle, say an electron, encounters a screen with two pin holes made in it, quantum physics says that the electron (under the suitable conditions which I won’t bore you with here) goes through both of the holes. So, it behaves like a wave, it interferes, even though it is a single particle. Electrons and all other particles can exist in two places (at two slits) at the same time.

Now, the way that Feynman (and more or less everyone else) would proceed to treat this mathematically is to say that there is one number, an amplitude, for the electron to go through one slit and there is another number, another amplitude, for it to go through the other slit. You add the two numbers up and that the modulus squared of it (the “modulus” is needed because amplitudes are in general complex numbers). That’s it. Two complex numbers suffice to describe the quantum behaviour of an electron.

So, where then are the infinite matrices? They are not needed here because we are talking about one electron only. However, the full quantum electron wave (which must include positrons too as Dirac taught us almost a hundred years ago) does indeed need infinity squared since one needs to be able to describe any number of electrons (and positrons, but I am simplifying a bit to make this digestible) that could potentially be there.

The two slit diffraction is then treated by adding together two infinity squared matrices. This described anything that can ever happen to any state of the electron field possible according to quantum mechanics. The result is another infinity squared matrix whose individual elements correspond to all possible interferences that can happen when the electron field encounters the two slits!

If we know that our experiment will only have one electron, and the possibility for more electrons to be created is miniscule and can be ignored, then we just have to look at one matrix element that contains that relevant entry corresponding to one electron only. And, it’s here that we get the identical result to the one using just the amplitudes and as you would find in Feynman’s Lectures of Physics (and many other place).

But, if you thought that the infinity square is bad, you ain’t seen nothing. Not only does every point in space require a number of infinity-squared entities, but there is (now a continuous) infinity of these points in the three-dimensional space (so basically another infinity-cubed multiplying the first infinity-squared). And, these matrices need to be specified at every instance of time through the wave equation I described earlier (or otherwise).

Why am I telling you about all this? Because I want to conclude by briefly commenting on some problems with this treatment of the fundamental entities in the universe. It is by far the most successful and accurate theory we’ve ever had of all the phenomena around us, but – like I said – it’s certainly not without its own problems.

For starter, most quantities we compute come out as being infinite (not a surprize given what we said above). The mass of the electron? Infinite. The charge of the electron? Infinite. The number of low energy photons emitted by a cascading electron? Infinite. The self-energy of photons? Infinite. And so on, you name it and more or less anything one computes ends up being infinite.

There are then sophisticated techniques to throw away these infinities to get finite results (called “renormalization”, a fancy name that masks the dodginess of this procedure). These have meet with a huge experimental success, however, conceptually speaking they leave us in the dark about what exactly is going on at that level of description.

Dirac (and many other great physicists) have been very dissatisfied with the state of affairs pertaining to quantum waves. Here is what he had to say: “Renormalization is just a stop-gap procedure. There must be some fundamental change in our ideas, probably a change just as fundamental as the passage from Bohr’s orbit theory to quantum mechanics. When you get a number turning out to be infinite which ought to be finite, you should admit that there is something wrong with your equations, and not hope that you can get a good theory just by doctoring up that number.”

So, does the quantum wave description of everything contain the seeds of its own destruction? What lies beyond the “doctoring up” of numbers in our most successful account of nature? I don’t know, but what I love about physics is this. Take any “well-understood” phenomenon, anything at all, and if you dig more into it, you will without a doubt discover new things. Even if you’ve been told by all your teachers in school that something is completely understood, this is never really so in physics. Anything can be revisited and improved upon.

And my bet is therefore that the understanding of quantum waves will come from a simple and unexpected direction. My two cents? Static interactions between charges. In other words, understanding exactly how two electrons repel one another through the electromagnetic field. Yes, this is another infinity that has to be renormalized in quantum field theory, after which we obtain the usual Coulomb law.

But, the infinite matrices are telling us that each electron creates infinitely many undetectable photons in the electromagnetic field, which then mediate the Coulomb force between the electrons, once we managed to regulate this infinity. The story seems non-sensical. And, many questions are left unanswered. Are the photons entangled to the electrons? Can this entanglement affect the quantum interference properties of the electrons? What is the rate at which it is created? And, above all, is it real, can it violate Bell’s inequalities and such?

Now, Feynman thought that the double slit contained all quantum mysteries; but Schrödinger said instead that entanglement is the characteristic feature of quantum physics. I side with Schrödinger which is why my money is on understanding the fundamental interactions through entanglement as a way to get to new physics.